Алгоритм построения КАМСИ-композиции

Выше, в Table 5 показан процесс последовательного кодирования и декодирования двух последовательно включенных КАМСИ А1 и А2. Рассмотрим теперь способ построения автомата, эквивалентного последовательному включению двух автоматов.

Алгоритм построения КАМСИ–композиции  из компонентов КАМСИ рассмотрим на примере  композиции двух автоматов.

Пример 3

Пусть заданы две КАМСИ

 и  (см. Table 7(а) и (b)). Следует построить таблицу переходов автомата ?, эквивалентного последовательному соединению  КАМСИ  .

		P,E1
	P=0		P=1
A		B,0		A,0
B		A,1		B,1

(a)

		Е1,E2
	P=0		P=1
A		A,1		B,1
B		B,0		A,0

(b)

?

P,E2

P=0

P=1

1

2

3

AA

BA,1

AA,1

AB

BB,0

AB,0

BA

AB,1

BB,1

BB

AA,0

BA,0

(c)

?		P,E2
	P=0		P=1
A		C,1		A,1
B		D,0		B,0
C		B,1		D,1
D		A,0		C,0

(d)

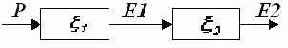
Table 7

P		1		1		0		1		0		0		1		1		0		0		1		0		0		1		1		1								(a)
?		A		A		A		C		D		A		C		D		C		B		D		C		B		D		C		D		C						(b)
				1		1		1		1		0		1		1		0		1		0		0		1		0		0		1		0						(c)
SS2				S0		S2		S4		S4		S4		S3		S2		S4		S3		S2		S3		S1		S2		S3		S1		S2		S3				(d)
						0		1		0		0		0		1		1		0		1		1		1		0		1		1		0		1				(e)
SS1						S0		S1		S2		S3		S1		S1		S2		S4		S3		S2		S4		S4		S3		S2		S4		S3		S2		(f)
								1		1		0		0		1		1		0		1		0		0		1		1		0		0		1		0		(g)

Table 8

Выполним следующую последовательность операций:

построить таблицу переходов, содержащую 2х2=4 ([33]) строки;

в первом столбце вписать все сочетания по два состояний КАМСИ

 и

 (первым стоит обозначение состояния

, а вторым –

);

на пересечении АА (см. Table 7(с))  и столбца Р=0 записать:

символ В (переход при Р=0 в КАМСИ

 из А в В, Е1=0);

символ А (переход при Е1=0 в КАМСИ

 из А в А, Е2=1);

через запятую записать значение Е2 равное 1; Аналогично заполнить остальные клетки столбцов 2 и 3.

построить Table 7(d). Для этого АА из Table 7(с) заменить: АА на А, АВ на В, ВА на С и ВВ на D ([34]).

Приведенный пример показывает, что если число компонентов КАМСИ  в композиции равно m, таблица переходов i-го  автомата имеет  состояний, то общее число N состояний композиции равно: N=n1…?ni…?nm;.

Примеры на стр. 43 и  46 позволяют сформулировать следующее утверждение:

Утверждение 2: «Последовательное соединение m компонентов КАМСИ эквивалентно КАМСИ-композиции, которая имеет µ-порядок, равный 

?= ?(1)… +.. ?(i)…+… ?(m);  (i:=1,m)

и таблицу переходов с N=n1…?ni…?nm; состояниями».

Доказательство этого Утверждения можно провести по индукции, если считать, что примеры на стр. 43 и  46 позволяют доказать  его для m=2. Далее, можно продолжить доказательство, увеличивая m на единицу.

Утверждение 2 позволяет сделать выводы, о том, что не всякая КАМСИ является КАМСИ-композицией, а только та, которая может быть представлена последовательностью компонент КАМСИ, отвечающих приведенному Утверждению.


Содержание раздела

---

---

---

Главная сайта

---