Какова же сложность построения КАМСИ-декодера?
Выше было показано, что для КАМСИ применим один из способов инвертирования: непосредственный и метод декомпозиции.
Для обоих этих методов выше были построены формулы для оценки сложности выполнения операций построения декодера и показано, что более просто применить метод непосредственного инвертирования.
Все ли так просто?
Обратимся к примеру КАМСИ-композиции, который мы рассматривали выше.
Пример 5
В Ошибка! Источник ссылки не найден. показаны примитивы





 |
P,E1 | ||||
|
P=0 |
P=1 | ||||
|
A |
B,0 |
A,0 | |||
|
B |
A,1 |
B,1 | |||
(a)
 |
Е1,E2 | ||||
|
P=0 |
P=1 | ||||
|
C |
C,1 |
D,1 | |||
|
D |
D,0 |
C,0 | |||
(b)
?
P,E2
P=0
P=1
1
2
3
AC
BC,1
AC,1
AD
BD,0
AD,0
BC
AD,1
BD,1
BD
AC,0
BC,0
(c)
|
? |
P,E2 | ||||
|
P=0 |
P=1 | ||||
|
A |
C,1 |
A,1 | |||
|
B |
D,0 |
B,0 | |||
|
C |
B,1 |
D,1 | |||
|
D |
A,0 |
C,0 | |||
(d)
SS1
P,E
E=0
E=1
S0
S1,1
S2,1
S1
S1,1
S2,1
S2
S3,0
S4,0
S3
S1,0
S2,0
S4
S3,1
S4,1
(e)
|
SS2 |
P,E | ||||
|
E=0 |
E=1 | ||||
|
S0 |
S1,0 |
S2,0 | |||
|
S1 |
S1,0 |
S2,0 | |||
|
S2 |
S3,1 |
S4,1 | |||
|
S3 |
S1,1 |
S2,1 | |||
|
S4 |
S3,0 |
S4,0 | |||
(f)
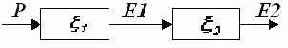
(g)
|
P |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
| |||||||||||||||||||
|
? |
A |
A |
A |
C |
B |
D |
C |
B |
B |
D |
C |
D |
A |
A |
C |
B |
|
| |||||||||||||||||||
|
E2 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
| ||||||||||||||||||||
|
SS2 |
|
S0 |
S2 |
S4 |
S4 |
S4 |
S3 |
S1 |
S2 |
S3 |
S1 |
S1 |
S2 |
S3 |
S2 |
S4 |
S4 | ||||||||||||||||||||
|
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 | ||||||||||||||||||||||
|
SS1 |
|
S0 |
S1 |
S2 |
S3 |
S1 |
S1 |
S2 |
S3 |
S2 |
S4 |
S3 |
S1 |
S2 |
S4 |
S4 |
S3 | ||||||||||||||||||||
|
|
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|||||||||||||||||||||
? |
P,E2 |
|
P=0 |
P=1 |
|
1 |
2 |
3 |
AC |
BC,1 |
AC,1 |
AD |
BD,0 |
AD,0 |
BC |
AD,1 |
BD,1 |
BD |
AC,0 |
BC,0 |
(a)
? |
P,E2 |
|
P=0 |
P=1 |
|
A |
C,1 |
A,1 |
B |
D,0 |
B,0 |
C |
B,1 |
D,1 |
D |
A,0 |
C,0 |
(b)
?
AC
AC/BC
AD
AD/BD
BC
AD/BD
BD
AC/BC
AC/BC
(AC/AD)(AC/BD)
(AD/BC)(BC/BD)
AD/BD
(AC/AD)(AC/BD)
(AD/BC)(BC/BD)
AC/AD
AC/BD
AD/BC
BC/BD
(c)
? |
||
A |
AC |
|
B |
BD |
|
C |
BD |
|
D |
AC |
|
AC |
(AB)(AD) (BC)(CD) |
|
BD |
(AB)(AD) (BC)(CD) |
|
AB |
||
AD |
||
BC |
||
CD |
||
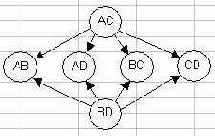
В Ошибка! Источник ссылки не найден. показан процесс построения тестирующего графа композиции ?. Как это видно из графа, его l=1, следовательно µ= l+2=3.
То есть, КАМСИ-композиция, в соответствии с тестирующим графом имеет µ=3, а «ведет себя», как µ=4 (см. Ошибка! Источник ссылки не найден.(h)).
Более того, для КАМСИ-композиции невозможно построить описанным в литературе способом инвертор. Это видно из Ошибка! Источник ссылки не найден.(b), где выходные последовательности 1101 и 1110 не могут появиться на выходе кодера, но инвертор должен быть определен на них (см. Ошибка! Источник ссылки не найден.(b) строки A1100 и A1111).
С другой стороны, так как известны инверсии КАМСИ



Информация, приведенная в этом разделе требует проведения дополнительных исследований.
Тем не менее, даже та информация, которая приведена, позволяет сделать следующие выводы:
A |
B |
C |
D |
|
0000 |
+ |
|||
0001 |
+ |
|||
0010 |
+ |
|||
0011 |
+ |
|||
0100 |
+ |
|||
0101 |
+ |
|||
0110 |
+ |
|||
0111 |
+ |
|||
1000 |
+ |
|||
1001 |
+ |
|||
1010 |
+ |
|||
1011 |
+ |
|||
1100 |
+ |
|||
1101 |
||||
1110 |
||||
1111 |
+ |
|||
P=0
P=1
(A1100)
(A1100),1
(A1101),1
(A1111)
(C1110),0
(A1111),1
(B0000)
(B0000),1
(B0001),1
(B0001)
(B0000),1
(B0001),1
(B0010)
(B0010),1
(B0011),1
(B0011)
(B0010),1
(B0011),1
(C1000)
(C1000),1
(C1001),0
(C1001)
(C1000),0
(C1001),0
(C1010)
(C1010),1
(C1011),0
(C1011)
(C1010),1
(C1011),0
(D0100)
(D0100),1
(D0101),0
(D0101)
(D0100),1
(D0101),0
(D0110)
(D0110),1
(D0111),0
(D0111)
(D0110),1
(D0111),0
(b)
Table 19

известен криптоаналитику.
SS1 |
P,E |
|
E=0 |
E=1 |
|
S0 |
S1,1 |
S2,1 |
S1 |
S1,1 |
S2,1 |
S2 |
S3,0 |
S4,0 |
S3 |
S1,0 |
S2,0 |
S4 |
S3,1 |
S4,1 |
SS2 |
P,E |
|
E=0 |
E=1 |
|
S0 |
S1,0 |
S2,0 |
S1 |
S1,0 |
S2,0 |
S2 |
S3,1 |
S4,1 |
S3 |
S1,1 |
S2,1 |
S4 |
S3,0 |
S4,0 |
SS2=>SS1
E,P
E=0
E=1
S0
S0S0
S1S1,1
S2S1,1
S1
S0S1
S1S1,1
S2S1,1
S2
S0S2
S1S3,0
S2S3,0
S3
S0S3
S1S1,0
S2S1,0
S4
S0S4
S1S3,1
S2S3,1
S5
S1S0
S1S1,1
S2S1,1
S6
S1S1
S1S1,1
S2S1,1
S7
S1S2
S1S3,0
S2S3,0
S8
S1S3
S1S1,0
S2S1,0
S9
S1S4
S1S3,1
S2S3,1
S10
S2S0
S3S2,1
S4S2,1
S11
S2S1
S3S2,1
S4S2,1
S12
S2S2
S3S4,0
S4S4,0
S13
S2S3
S3S2,0
S4S2,0
S14
S2S4
S3S4,1
S4S4,1
S15
S3S0
S1S2,1
S2S2,1
S16
S3S1
S1S2,1
S2S2,1
S17
S3S2
S1S4,0
S2S4,0
S18
S3S3
S1S2,0
S2S2,0
S19
S3S4
S1S4,1
S2S4,1
S20
S4S0
S3S1,1
S4S1,1
S22
S4S1
S3S1,1
S4S1,1
S23
S4S2
S3S3,0
S4S3,0
S24
S4S3
S3S1,0
S4S1,0
S25
S4S4
S3S3,1
S4S3,1

E,P
E=0
E=1
S0
S0S0
S6,1
S11,1
S1
S0S1
S6,1
S11,1
S2
S0S2
S8,0
S13,0
S3
S0S3
S6,0
S11,0
S4
S0S4
S8,1
S13,1
S5
S1S0
S1,1
S11,1
S6
S1S1
S6,1
S11,1
S7
S1S2
S8,0
S13,0
S8
S1S3
S6,0
S11,0
S9
S1S4
S8,1
S13,1
S10
S2S0
S17,1
S23,1
S11
S2S1
S17,1
S23,1
S12
S2S2
S19,0
S25,0
S13
S2S3
S17,0
S23,0
S14
S2S4
S19,1
S25,1
S15
S3S0
S7,1
S12,1
S16
S3S1
S7,1
S12,1
S17
S3S2
S9,0
S14,0
S18
S3S3
S7,0
S12,0
S19
S3S4
S9,1
S14,1
S20
S4S0
S16,1
S22,1
S22
S4S1
S16,1
S22,1
S23
S4S2
S18,0
S24,0
S24
S4S3
S16,0
S22,0
S25
S4S4
S18,1
S24,1
P |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
||
? |
A |
A |
A |
C |
B |
D |
C |
B |
B |
D |
C |
D |
A |
A |
C |
B |
|
E2 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
||
 |
S0 |
S11 |
S23 |
S24 |
S22 |
S16 |
S7 |
S13 |
S17 |
S9 |
S8 |
S11 |
S17 |
S14 |
S25 |
S24 |
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|||
P |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |