Для выполнения этого определения можно модифицировать протокол A-GDH.2 в следующий:
  Этап i (0< i <n): 1. Mi получает множество промежуточных величин { Vk | 1£ k £ n}. (в данном контексте можно сказать, что M1 получает пустое множество на первом этапе): a (r1…ri-1 / rk)(K k1…K k(i-1)) при k £ (i-1) Vk = a (r1…ri-1)(K k1…K k(i-1)) при k > (i-1) . 2. Mi обновляет каждое Vk следующим образом: (Vk ) riK ik = a (r1…ri / rk)(K k1…K ki) при k < i Vk = (Vk ) riK ik = a (r1…ri)(K k1…K ki) при k > i . Vk при k = i (Замечание: на первом этапе M1 выбирает V1 = a .) Этап n: 1. Mn рассылает множество всех Vk участникам группы. 2. При получении Mi выбирает свое Vi =a (r1…rn / ri)(K1i…K ni). Mi вычисляет (Vk ) ri(K1i-1… K ni-1)= a r1…rn . Заметим, что вместо того, чтобы вычислять n обратных элементов, Mi может вычислять 1 обратный элемент Pi-1=(K1i-1… Kni-1), где Pi=(K1i… Kni). |
В протоколе SA-GDH.2 требуется, чтобы каждый участник группы имел некоторый общий ключ с любым другим участником (это значение Kji). Однако, как уже было замечено для каждого такого ключа Kji не требуется нахождение обратного Kji-1. Таким образом, достаточно получить такие ключи перед началом работы в группе и затем эти ключи могут оставаться постоянными, не добавляя лишних действий в протокол.
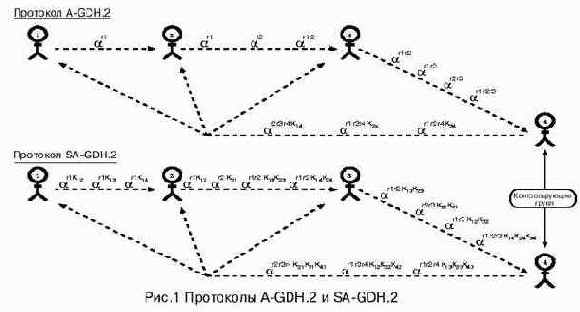
Протокол основан на кольцевой схеме взаимодействия, т.е. данные проходят по кругу и лишь на последнем этапе идет широковещательная рассылка. Данные, которые передаются, представляют собой множество из n элементов. i-й элемент содержит своеобразное «накопление ключа» для i-го участника. Во время обновления ключа каждый из участников вносит свой вклад в формирование ключа. Только пройдя полный круг, i-й элемент множества будет иметь вклады всех участников и их секретные ключи для связи с i-м абонентом (рис. 1). Это позволяет избежать явной замены противником одного из значений на какое-то другое, выгодное ему (возможное вмешательство противника рассмотрим далее)
Однако SA-GDH.2 имеет более высокую «вычислительную стоимость» по сравнению с A-GDH.2. Прежде всего, он требует (n-1) экспоненцирование для каждого Mi (кроме первого), в отличие от i
экспоненцирований в A-GDH.2. К этому еще добавляется работа по формированию общих ключей для каждой пары абонентов (если они не вычислены заранее): на последнем этапе проводится одно экспоненцирование – как и в A-GDH.2. На рис. 1 приведены примеры протоколов A-GDH.2 и SA-GDH.2.
Как показано в [1], протокол SA-GDH.2 обеспечивает полную аутентификацию группового ключа.
Теорема 2.2.1 Протокол SA-DH обеспечивает полную аутентификацию группового ключа.
Док-во: предположим, Mi и Mj вычислили одинаковый ключ в результате выполнения протокола. Пусть Kn=Sn(Mi)=Sn(Mj), и предположим, что некто Mp ÎM (p¹i,j) не сделал вклада в этот ключ. Пусть Vi и Vj обозначают величины, полученные Mi и Mj на последнем этапе протокола. Напомним, что в соответствии с протоколом
Sn(Mi)=(Vi)(K1i-1…Kni-1)ri и Sn(Mj)=(Vj)(K1j-1…Knj-1)rj .
Поскольку все участники группы сделали вклад в ключ, то можно записать, что
Vi=a
(r1…rn/rpri)(K1i-1…Kni-1/Kpi-1)
(для Vj аналогично), и
Sn(Mi)= a (r1…rn/rp)Kpi-1, что должно равняться Sn(Mj)= a
(r1…rn/rp)Kpj-1.
Но поскольку Kpi-1
и Kpj-1
являются секретными, то получаем противоречие. #
В работе [1] также отмечается, что обсуждаемый протокол обладает устойчивостью к атакам по известному ключу (known key attacks), однако строгого формального доказательства не приведено, авторы лишь отмечают, что это легко пронаблюдать на приведенной выше атаке на A-GDH.2.